7 Object-Oriented Programming in Python
Object-Oriented Programming (OOP) is a programming paradigm that allows you to model real-world objects, concepts, and relationships between them in your code. Python is a multi-paradigm language that supports OOP, among other programming paradigms.
In Python, you can create classes, which are blueprint templates for creating objects, and objects, which are instances of a class. A class can have attributes, which are variables that hold data, and methods, which are functions that operate on that data.
We will begin by importing the necessary libraries.
# third-party imports
import pandas as pd # used for most data frame operations
import numpy as np # for linear algebra functionality
import matplotlib.pyplot as plt # import plotting library
import re # for regex functionality
import os # for interacting with the operating system
from tabulate import tabulate # for tables
# import sklearn's 'metrics' module, providing functions for
# evaluating the model prediction quality, like precision, recall,
# confusion matrix, ROC curve etc.
from sklearn import metrics
from sklearn.metrics import (
average_precision_score,
precision_recall_curve,
auc,
roc_curve,
classification_report,
recall_score,
precision_score,
roc_auc_score,
brier_score_loss,
confusion_matrix
)To create a class in Python, you use the class keyword followed by the name of the class, and you define its attributes and methods within it. For example:
class Person:
def __init__(self, name, age):
self.name = name
self.age = age
def say_hello(self):
print(f"Hello, my name is {self.name} and I'm {self.age} years old.")In this example, we defined a Person class with two attributes, name and age, and a method say_hello that prints a greeting using those attributes.
To create an object of this class, you use the class name followed by parentheses, and pass any necessary arguments to the constructor method (the __init__ method in this case):
Hello, my name is Alice and I'm 30 years old.This code creates a Person object named person with the name “Alice” and age 30, and then calls its say_hello method, which prints “Hello, my name is Alice and I’m 30 years old.”
In OOP, you can also define inheritance relationships between classes, where a child class (also known as a subclass) inherits attributes and methods from a parent class (also known as a superclass), and can also define its own attributes and methods. This allows you to reuse code and create more specialized objects.
Here’s an example of inheritance in Python:
class Student(Person):
def __init__(self, name, age, major):
super().__init__(name, age)
self.major = major
def say_hello(self):
print(f"Hello, my name is {self.name} and I'm a {self.major} major.")In this example, we defined a Student class that inherits from the Person class and adds a major attribute and a new version of the say_hello method that includes the major in the greeting.
You can create a Student object in the same way as a Person object, and it will have access to both the Person and Student attributes and methods:
Hello, my name is Bob and I'm a Computer Science major.This code creates a Student object named student with the name “Bob”, age 20, and major “Computer Science”, and then calls its say_hello method, which prints “Hello, my name is Bob and I’m a Computer Science major.”
7.1 Class Attributes vs. Instance Attributes
In object-oriented programming (OOP), classes are used to define a blueprint for creating objects. A class can have attributes, which are variables that hold data, and methods, which are functions that operate on that data.
In Python, there are two types of attributes in a class: class attributes and instance attributes.
Class attributes are attributes that belong to the class itself, rather than any particular instance of the class. They are shared among all instances of the class, and are usually defined outside of any method of the class. Class attributes are accessed using the class name, rather than an instance of the class.
Here’s an example:
In this example, species is a class attribute that is shared by all instances of the Person class. It is defined outside of the constructor method, and can be accessed using the class name: Person.species.
Instance attributes, on the other hand, are attributes that belong to a particular instance of a class. They are unique to each instance, and are defined within the constructor method of the class. Instance attributes are accessed using the name of the instance followed by a dot and the name of the attribute.
Here’s an example:
In this example, name and age are instance attributes that belong to each individual instance of the Person class. They are defined within the constructor method, and are accessed using the name of the instance: person.name or person.age, where person is an instance of the Person class.
It’s important to note that instance attributes can be modified on a per-instance basis, while class attributes are shared among all instances and should not be modified for individual instances.
In summary, class attributes are shared among all instances of a class and are accessed using the class name, while instance attributes are unique to each instance of a class and are accessed using the instance name.
7.2 Data Science Applications
To introduce some fundamental data science concepts, we use the Chronic Kidney Disease (CKD) Dataset.
7.3 Creating a custom data structure
In data science, you may come across data that doesn’t fit neatly into a table or array. In this case, you can create a custom data structure using OOP to represent the data in a way that makes sense for your analysis.
For example, you could create a DemographicInfo class to represent data about patients’ demographic information with CKD. This class might have attributes such as age, hyptertension, diabetes, coronary artery disease, and other relevant attributes and methods to analyze or manipulate this data.
class DemographicInfo:
def __init__(self, age, htn, dm, cad):
self.age = age
self.htn = htn
self.dm = dm
self.cad = cad
class LabResults:
def __init__(self, bp, sg, al, su, rbc, pc, pcc, ba, bgr, bu, sc, sod, pot,
hemo, pcv, wc, rc):
self.bp = bp
self.sg = sg
self.al = al
self.su = su
self.rbc = rbc
self.pc = pc
self.pcc = pcc
self.ba = ba
self.bgr = bgr
self.bu = bu
self.sc = sc
self.sod = sod
self.pot = pot
self.hemo = hemo
self.pcv = pcv
self.wc = wc
self.rc = rc
class Symptoms:
def __init__(self, appet, pe, ane):
self.appet = appet
self.pe = pe
self.ane = aneAfter separating the data fields into three separate classes, we will use instances of these classes as attributes of the CKDPatient class. The get_* methods can still be used to retrieve indvidual attributes as needed.
class CKDPatient:
def __init__(self, demographic_info, lab_results, symptoms, classification):
self.demographic_info = demographic_info
self.lab_results = lab_results
self.symptoms = symptoms
self.classification = classification
def get_age(self):
return self.demographic_info.age
def get_bp(self):
return self.lab_results.bp
def get_sg(self):
return self.lab_results.sg
# add getters for other attributes as neededTo create a CKDPatient object with this implementation, we can instantiate the relevant classes and pass them to the CKDPatient constructor:
demo_info = DemographicInfo(age=48, htn="yes", dm="yes", cad="no")
lab_results = LabResults(bp=80, sg=1.02, al=1, su=0, rbc="normal", pc="normal",
pcc="notpresent", ba="notpresent", bgr=121, bu=36,
sc=1.2, sod=137, pot=4.4, hemo=15.4, pcv=44, wc=7800,
rc=5.2)
symptoms = Symptoms(appet="good", pe="no", ane="no")
patient1 = CKDPatient(demographic_info=demo_info, lab_results=lab_results,
symptoms=symptoms, classification="ckd")Now, let’s go ahead and update the implementation of the CKDPatient class with modularized data fields using get_* methods that can be used to retrieve individual attributes of a CKDPatient object.
For example, the get_age method returns the age of the patient:
Patient 1 is 48 years old.class KFRE_Patient:
def __init__(self, age, male, eGFR, ACR, region='north'):
self.age = age
self.male = male
self.eGFR = eGFR
self.ACR = ACR
self.region = region
def predict_risk(self):
alpha = 0.9750 if self.region == 'north' else 0.9832
return 1 - alpha ** np.exp(
-0.2201 * (self.age / 10 - 7.036) +
0.2467 * (self.male - 0.5642) -
0.5567 * (self.eGFR / 5 - 7.222) +
0.4510 * (np.log(self.ACR) - 5.137)
)0.59618706847982627.4 Creating a Machine Learning Model
In data science, machine learning models may need to be reused across multiple projects. To this end, OOP can be used to create a Model class that can be trained and used to make predictions on new data. On a basic level, the structure is as follows:
class Model:
def __init__(self):
# initialize the model
pass
def train(self, X, y):
# train the model on the given data
pass
def predict(self, X):
# make predictions on new data using the trained model
passThis model class allows us to create different types of machine learning models by subclassing this class and implementing the train and predict methods for each specific model.
# open path to data folder and parse the file
with open(data_folder + 'chronic_kidney_disease.arff') as f:
lines = f.readlines()
selected_lines = lines[29:545] # Extract lines 28 to 544 (index starts at 0)import pandas as pd # import the pandas library for data science
import io # library for input/output formats
# Convert the list into a single string with newline characters
data_str = '\n'.join(selected_lines)
# Split the data_str into lines
lines = data_str.split("\n")
# Filter out lines with an incorrect number of fields
correct_lines = [line for line in lines if len(line.split(',')) == 25]
# Join the lines back into a single string
correct_data_str = '\n'.join(correct_lines)
# Parse into pandas DataFrame
df = pd.read_csv(io.StringIO(correct_data_str), header=None,
names=['age', 'bp', 'sg', 'al', 'su', 'rbc', 'pc', 'pcc', 'ba',
'bgr', 'bu', 'sc', 'sod', 'pot', 'hemo', 'pcv', 'wbcc',
'rbcc', 'htn', 'dm', 'cad', 'appet', 'pe', 'ane',
'class'], na_values=['?']) age bp sg al su rbc ... dm cad appet pe ane class
0 48.0 80.0 1.020 1.0 0.0 NaN ... yes no good no no ckd
1 7.0 50.0 1.020 4.0 0.0 NaN ... no no good no no ckd
2 62.0 80.0 1.010 2.0 3.0 normal ... yes no poor no yes ckd
3 48.0 70.0 1.005 4.0 0.0 normal ... no no poor yes yes ckd
4 51.0 80.0 1.010 2.0 0.0 normal ... no no good no no ckd
[5 rows x 25 columns]7.4.1 Patient de-identification and PHI
It is crucial to note that the patient IDs we are about to discuss are completely fictitious, randomly generated numbers attributed to each patient for the purposes of this dataset. These fabricated IDs bear no relation to any actual, identifiable information about the patient.
These fake patient IDs serve as a crucial pillar in medical data management. Uniquely assigned to each patient, they ensure the anonymity of individuals in a dataset, thereby adhering to Protected Health Information (PHI) norms. PHI norms, integral to healthcare data regulations like HIPAA, mandate the protection of identifiable information like names, addresses, and social security numbers. By assigning a unique, anonymous ID to each patient, we can store and access their data without directly handling or exposing this sensitive information.
Using these fake patient IDs also allows for seamless data integration across multiple dataframes or datasets. This integration is often achieved via an “inner join”, a method that combines two dataframes based on a common key column (here, the patient ID), resulting in a new dataframe that includes only those records where the patient ID exists in both original dataframes.
Creating and using these completely fabricated patient IDs enables us to maintain data privacy, and it’s also pivotal for secure and efficient data handling in healthcare. By joining data from different sources, we enhance data integrity and completeness, enabling comprehensive patient profiling and leading to more accurate data analysis. This can result in improved patient care, more accurate disease prediction, efficient treatment planning, and advancement in medical research.
The following function appends a unique, 9-digit string ID to each row in a given pandas DataFrame, df, using a reproducible random process determined by a seed value (defaulted to 222). It creates the ID by joining together a random selection from 0-9 digits. This new Patient_ID column is then set as the DataFrame’s index. The function returns the updated DataFrame with the newly created Patient_ID column. Note that for large dataframes, there’s a low, yet non-zero, chance of ID collision. Also, these are string representations of IDs, not numerical ones.
import random # for generating random numbers and performing random operations.
def add_patient_ids(df, seed=222):
"""
Add a column of unique, 9-digit patient IDs to the dataframe.
This function sets a random seed and then generates a 9-digit patient ID for
each row in the dataframe. The new IDs are added as a new 'Patient_ID'
column, which is placed as the first column in the dataframe.
Args:
df (pd.DataFrame): The dataframe to add patient IDs to.
seed (int, optional): The seed for the random number generator.
Defaults to 222.
Returns:
pd.DataFrame: The updated dataframe with the new 'Patient_ID' column.
"""
random.seed(seed)
# Generate a list of unique IDs
patient_ids = [''.join(random.choices('0123456789', k=9))
for _ in range(len(df))]
# Create a new column in df for these IDs
df['Patient_ID'] = patient_ids
# Make 'Patient_ID' the first column and set it to index
df = df.set_index('Patient_ID')
return df age bp sg al su rbc ... dm cad appet pe ane class
Patient_ID ...
723027400 48.0 80.0 1.020 1.0 0.0 NaN ... yes no good no no ckd
904532344 7.0 50.0 1.020 4.0 0.0 NaN ... no no good no no ckd
890205650 62.0 80.0 1.010 2.0 3.0 normal ... yes no poor no yes ckd
317865962 48.0 70.0 1.005 4.0 0.0 normal ... no no poor yes yes ckd
968356501 51.0 80.0 1.010 2.0 0.0 normal ... no no good no no ckd
[5 rows x 25 columns]7.4.2 Feature Engineering
The goal of the following endeavor is to replicate the research conducted by Tangri et al. on chronic kidney disease (CKD) using feature engineering techniques. Specifically, we aim to incorporate randomized values for newly created sex, estimated glomerular filtration rate (eGFR), and urine albumin-to-creatinine ratio (uACR) columns. These engineered features will be appended this 400 row dataset. Although this endeavor may not have clinical relevance in terms of creating data that aligns with a clinically relevant context, it is still valuable for the purpose of reproducibility.
By introducing randomized values for the sex, eGFR, and uACR columns, we can explore their potential impact on predicting CKD. The randomized sex feature allows us to evaluate the influence of sex on the prediction model. The eGFR and uACR columns provide important indicators of kidney function and health, and by manipulating them, we can investigate their relationship with CKD.
By conducting this replication study, we aim to gain insights into the significance of these engineered features in predicting CKD. This research has the potential to contribute to the understanding and development of more accurate predictive models for CKD diagnosis and management, ultimately leading to improved patient care and outcomes in the field of nephrology.
\[1 - 0.9750 ^ {\exp \left(-0.2201 \times \left(\frac{{\text{age}}}{10} - 7.036\right) + 0.2467 \times \left(\text{male} - 0.5642\right) - 0.5567 \times \left(\frac{{\text{eGFR}}}{5} - 7.222\right) + 0.4510 \times \left(\log(\text{ACR}) - 5.137\right)\right)}\]
One way to incorporate Object-Oriented Programming (OOP) into this process is by creating a class that encapsulates all the feature engineering steps. This class would have methods for each step of the process, which can be called in a sequence.
class FeatureEngineer:
"""
Class for performing feature engineering on a dataset.
This class provides methods for each feature engineering step,
and a `process` method to run all steps in sequence.
"""
def __init__(self, df):
"""
Initialize the feature engineer with a dataframe.
"""
self.df = df.copy()
np.random.seed(222) # Set seed for reproducibility
def filter_by_class(self):
"""
Filter dataframe by 'ckd' class.
"""
self.df = self.df[self.df['class'] == 'ckd']
return self
def impute_age(self):
"""
Impute missing 'age' values with the mean age.
"""
self.df['age'] = self.df['age'].fillna(self.df['age'].mean())
return self
def create_sex_cat(self):
"""
Create 'sex_cat' column with randomly generated binary values.
"""
self.df['sex_cat'] = np.random.choice([0, 1], size=(len(self.df)))
return self
def create_eGFR(self):
"""
Create 'eGFR' column with randomly generated values between 1 and 59.
"""
self.df['eGFR'] = np.random.uniform(1, 59, size=len(self.df))
return self
def create_uACR_and_log(self):
"""
Create 'uACR' and 'log_uACR' columns with randomly generated values.
"""
self.df['uACR'] = np.random.uniform(0, 400, size=len(self.df))
self.df['log_uACR'] = np.log(self.df['uACR'])
return self
def assign_region(self):
"""
Assign random 'Region' values to each row.
"""
region_choices = ['North American', 'Non-N.American']
self.df['Region'] = np.random.choice(region_choices, size=len(self.df))
return self
def create_sex(self):
"""
Convert 'sex_cat' to 'sex' with 'male' or 'female' values.
"""
self.df['sex'] = self.df['sex_cat'].replace({0: 'male', 1: 'female'})
return self
def binarize_dm_and_htn(self):
"""
Convert 'dm' and 'htn' columns to binary values.
"""
self.df['dm'] = (self.df['dm'].replace({True: 'yes', False: 'no'})
.astype(str).str.strip()
.replace({'yes': 1,'no': 0})
.fillna(0).astype(int))
self.df['htn'] = (self.df['htn'].replace({True: 'yes', False: 'no'})
.astype(str).str.strip()
.replace({'yes': 1,'no': 0})
.fillna(0).astype(int))
return self
def process(self):
"""
Run all feature engineering steps in sequence and return the result.
"""
(self.filter_by_class()
.impute_age()
.create_sex_cat()
.create_eGFR()
.create_uACR_and_log()
.assign_region()
.create_sex()
.binarize_dm_and_htn())
return self.df# Instantiate the FeatureEngineer class with df as the input DataFrame
engineered = FeatureEngineer(df)
# Call the 'process' method to perform all feature engineering steps and assign
# the result to processed_df
df = engineered.process() age bp sg ... log_uACR Region sex
Patient_ID ...
723027400 48.0 80.0 1.020 ... 5.364914 North American male
904532344 7.0 50.0 1.020 ... 4.383044 Non-N.American female
890205650 62.0 80.0 1.010 ... 5.478338 Non-N.American female
317865962 48.0 70.0 1.005 ... 5.653522 North American male
968356501 51.0 80.0 1.010 ... 5.802650 Non-N.American male
[5 rows x 31 columns]7.4.3 Assigning CKD Stage Based on eGFR
The assign_ckd_stage(eGFR) function is necessary to determine the stage of chronic kidney disease (CKD) based on the provided estimated glomerular filtration rate (eGFR). CKD is a progressive condition that affects kidney function, and its severity is categorized into different stages based on eGFR values. By using this function, we can easily determine the appropriate CKD stage for a given eGFR value.
The function helps in classifying patients into specific stages, such as Stage 3, Stage 4, or Stage 5, based on the eGFR value provided as an input. This classification is crucial for appropriate diagnosis, treatment planning, and monitoring of patients with CKD. It allows healthcare professionals to understand the level of kidney impairment and adapt their management strategies accordingly.
Moreover, the function also handles cases where the provided eGFR value is negative or greater than or equal to 60. Negative values are likely errors or missing data, and assigning Unknown for these cases helps identify and address such issues. Similarly, for eGFR values greater than or equal to 60, CKD is not typically diagnosed, and assigning Unknown helps indicate that these cases may require further evaluation or investigation.
def assign_ckd_stage(eGFR):
"""
Assigns CKD stage based on eGFR (estimated glomerular filtration rate).
Args:
eGFR (float): Estimated glomerular filtration rate.
Returns:
str: CKD stage based on eGFR value:
- 'Stage 3': eGFR >= 30 and < 60
- 'Stage 4': eGFR >= 15 and < 30
- 'Stage 5': eGFR < 15 and >= 0
- 'Unknown': Negative eGFR or eGFR >= 60 (not typical for CKD).
"""
if eGFR >= 30 and eGFR < 60:
return 'Stage 3'
elif eGFR >= 15 and eGFR < 30:
return 'Stage 4'
elif eGFR < 15 and eGFR >= 0:
return 'Stage 5'
elif eGFR < 0: # values of eGFR can't be negative,
return 'Unknown' # it's probably an error or missing value
else:
return 'Unknown' # for eGFR >= 60, CKD is not typically diagnosed,
# we put 'Unknown' for these casesdf['CKD_stage'] = df['eGFR'].apply(assign_ckd_stage)
# uses the apply function to apply a lambda function to each element in the
# 'CKD_stage' column. If the value of the element is 'Stage 5', then 'ESRD' is
# returned, otherwise 'Not ESRD' is returned. The result is stored in a new
# column named 'ESRD_status'.
df['ESRD_status'] = df['CKD_stage'].apply(
lambda x: 'ESRD' if x == 'Stage 5' else 'Not ESRD')
# Assign ESRD_Outcome column by replacing 'Not ESRD' with 0 and 'ESRD' with 1
df['ESRD_Outcome'] = df['ESRD_status'].replace({'Not ESRD': 0, 'ESRD': 1})Index(['age', 'bp', 'sg', 'al', 'su', 'rbc', 'pc', 'pcc', 'ba', 'bgr', 'bu',
'sc', 'sod', 'pot', 'hemo', 'pcv', 'wbcc', 'rbcc', 'htn', 'dm', 'cad',
'appet', 'pe', 'ane', 'class', 'sex_cat', 'eGFR', 'uACR', 'log_uACR',
'Region', 'sex', 'CKD_stage', 'ESRD_status', 'ESRD_Outcome'],
dtype='object')7.4.4 Reproducing Tangri et al.’s Risk Predictions
The risk_pred function is necessary to calculate the risk prediction for an individual based on various parameters. This function aims to reproduce Tangri et al.’s work on the equations involving four and six variables.
The function takes multiple input parameters such as age, sex, eGFR (estimated Glomerular Filtration Rate), uACR (Urinary Albumin-to-Creatinine Ratio), Region (geographical region), dm (diabetes mellitus status), htn (hypertension status), and years (duration for which the risk is being predicted). These parameters are used in the risk calculation equation, where different coefficients are applied based on the region and duration.
By utilizing the provided parameters and applying the corresponding coefficients, the function calculates the risk prediction. The risk prediction represents the estimated risk of a specific outcome, which could be related to chronic kidney disease or other health conditions. The calculated risk prediction value helps in assessing the likelihood of an adverse event occurring within the specified duration.
The function includes conditionals to determine the value of alpha (a coefficient) based on the provided region and duration. It also considers optional parameters for dm and htn, calculating their respective factors if the information is provided or setting them to zero if not available.
The resulting risk prediction is returned as a float value, representing the estimated risk for the given individual based on the provided parameters.
def risk_pred(age, sex, eGFR,
uACR, Region,
dm=None, htn=None,
years=2):
"""
This function calculates the risk prediction based on various parameters.
Different coefficients are used in the calculation based on the geographical
region and the duration (in years) for which the risk is being predicted.
Parameters:
Age (float): Age of the individual.
Sex (float): Biological sex of the individual, usually coded as 1 for male
and 0 for female.
entry_egfrckdepi2009_mean (float):
Mean eGFR (estimated Glomerular Filtration Rate) value.
entry_uacr_mean (float): Mean uacr (Urinary Albumin-to-Creatinine Ratio)
value.
Region (str): Geographical region of the individual
('North American' or other).
entry_dmid_flag (float, optional):
Diabetes mellitus status of the individual.
entry_htnid_flag (float, optional):
Hypertension status of the individual.
years (int, optional):
Duration for which the risk is being predicted, either 2 or 5 years.
Returns:
risk_prediction (float): Calculated risk prediction.
"""
# Determine the value of alpha based on the region and the duration
if years == 2:
alpha = np.where(Region == 'North American',
0.9750, 0.9832)
elif years == 5:
alpha = np.where(Region == 'North American',
0.9240, 0.9365)
else:
# Raise an error if an invalid duration is provided
raise ValueError("Invalid years value. Choose 2 or 5.")
# Calculate the diabetes factor, or set it to 0 if no diabetes
# information is provided
dm_factor = 0 if dm is None else \
-0.1475 * (dm - 0.5106)
# Calculate the hypertension factor, or set it to 0 if no
# hypertension information is provided
htn_factor = 0 if htn is None else \
0.1426 * (htn - 0.8501)
# Return the calculated risk prediction
return 1 - alpha**np.exp(
- 0.2201 * (age/10 - 7.036)
+ 0.2467 * (sex - 0.5642)
- 0.5567 * (eGFR/5 - 7.222)
+ 0.4510 * (np.log(uACR) - 5.137)
+ dm_factor
+ htn_factor
)7.4.5 Creating a Risk Predictor Class
The risk_pred function is passed into the RiskPredictor class to provide a convenient and organized way of using the risk prediction model for chronic kidney disease (CKD). The class serves as a wrapper around the risk_pred function, providing additional functionality and encapsulation.
The RiskPredictor class represents a risk predictor for CKD. It has two main attributes: data, which holds the patient data in a DataFrame format, and Sex, which represents the sex of the patients, derived from the data.
The class has a predict method that takes two parameters: years and use_extra_vars. The years parameter specifies the number of years for which the risk of CKD is predicted, and use_extra_vars is an optional boolean parameter that determines whether extra variables (diabetes and hypertension status) should be used in the prediction.
In the constructor (__init__), the RiskPredictor object is initialized with the patient data and the column name (sex) in the data that represents the sex of the patients. The sex column is then processed to create the sex attribute, which holds a Series representing the sex of the patients, specifically as a boolean value indicating if the patient is male (True) or not (False).
The predict method uses the risk_pred function to calculate the risk of CKD based on the provided parameters. If use_extra_vars is True, the additional variables (diabetes and hypertension status) are included in the prediction by passing them as arguments to risk_pred. Otherwise, only the essential parameters (age, sex, eGFR, uACR, and Region) are used.
By encapsulating the risk_pred function within the RiskPredictor class, it provides a higher level of abstraction and simplifies the process of using the risk prediction model. The class allows for easier handling of patient data, such as accessing the data and specifying the prediction duration and usage of extra variables.
class RiskPredictor:
"""
A class to represent a risk predictor for chronic kidney disease (CKD).
This class uses the Tangri risk prediction model, which calculates risk
based on various patient parameters. Results are accurate for both males
and females, but the original paper calculated risk specifically for males.
Attributes:
data (DataFrame): The patient data.
Sex (Series): The sex of the patients, determined from the data.
Methods:
predict(years, use_extra_vars): Predicts the risk of CKD for the given
number of years, optionally using extra
variables for the prediction.
"""
def __init__(self, data, sex):
"""
Constructs the necessary attributes for the RiskPredictor object.
Parameters:
data (DataFrame): The patient data.
Sex (str): Column name in the data for the sex of the patients.
"""
self.data = data
self.sex = self.data[sex]=='male'
def predict(self, years, use_extra_vars=False):
"""
Predicts the risk of CKD for the given number of years, optionally using
extra variables for the prediction.
Parameters:
years (int): The number of years for which to predict the risk.
use_extra_vars (bool, optional): Whether to use extra variables
(diabetes and hypertension status)
for the prediction.
Returns:
risk_prediction (float): The predicted risk of CKD.
"""
if use_extra_vars:
return risk_pred(
self.data['age'],
self.sex,
self.data['eGFR'],
self.data['uACR'],
self.data['Region'],
self.data['dm'],
self.data['htn'],
years=years
)
else:
return risk_pred(
self.data['age'],
self.sex,
self.data['eGFR'],
self.data['uACR'],
self.data['Region'],
years=years
)
# Create an instance of RiskPredictor
predictor = RiskPredictor(df, 'sex')
# Predict risk for different combinations of years and variables
pred_4var_2year = predictor.predict(years=2)
pred_4var_5year = predictor.predict(years=5)
pred_6var_2year = predictor.predict(years=2, use_extra_vars=True)
pred_6var_5year = predictor.predict(years=5, use_extra_vars=True)
# inner join the different combinations of years and variables to
# kfre_inclusion dataframe
df = df.assign(
pred_4var_2year=pred_4var_2year,
pred_4var_5year=pred_4var_5year,
pred_6var_2year=pred_6var_2year,
pred_6var_5year=pred_6var_5year,
)7.4.6 Performance Assessment of Predictive Models
After determining the CKD stage based on eGFR and calculating the risk predictions, it’s critical to evaluate the performance of these predictive models. This is where our PerformanceAssessment class comes into play.
The PerformanceAssessment class is a robust tool designed to assess the efficacy of our predictive models. It provides a structured way to evaluate the performance of models using two commonly applied methods in the field of machine learning and statistical modeling - the Receiver Operating Characteristic (ROC) curve and various performance metrics, such as precision, recall, AUC ROC, and Brier score.
The class constructor takes in a dataframe and an outcome variable. The dataframe contains the prediction variables and the actual outcome data, while the outcome variable is the true outcome we’re interested in predicting.
The plot_roc_curve method in the class plots the ROC curve(s) for one or more prediction variables. An ROC curve is a graphical representation that illustrates the diagnostic ability of a binary classifier system. It’s created by plotting the True Positive Rate (Sensitivity) against the False Positive Rate (1 - Specificity) at various threshold settings. The AUC (Area Under The Curve) ROC gives a single measure of performance of the prediction at all threshold levels. Higher the AUC, better the model is at distinguishing between patients with the disease and no disease.
In the report_metrics method, it calculates several performance metrics for each predictive variable, including precision, recall, AUC ROC, AUC PR (Precision Recall), average precision, sensitivity, specificity, and Brier score. These metrics provide a comprehensive assessment of the prediction performance. For instance, precision gives the proportion of true positive predictions among all positive predictions, recall gives the proportion of true positive predictions among all actual positives, and the Brier score measures the mean squared difference between the predicted probability of an event and the actual outcome.
By integrating these features into a single class, PerformanceAssessment streamlines the model evaluation process, making it easier to assess and compare the performance of different predictive models in the context of CKD risk prediction. This class is an invaluable tool in the predictive modeling process, enabling us to quantify the effectiveness of our models and facilitating informed decision-making when it comes to selecting the most suitable model.
class PerformanceAssessment:
"""
A class used to assess the performance of predictive models.
Attributes
----------
df : pandas.DataFrame
The dataframe containing the outcome and prediction variables.
outcome_col : str
The name of the outcome variable in the dataframe.
Methods
-------
plot_roc_curve(*pred_var_names)
Plots the ROC curve(s) for the provided predictive variable(s).
report_metrics(pred_var_names)
Calculates and reports various performance metrics for the provided
predictive variable(s).
"""
def __init__(self, df, outcome_col):
"""
Constructs all the necessary attributes for the PerformanceAssessment
object.
Parameters:
df : pandas.DataFrame
The dataframe containing the outcome and prediction variables.
outcome_col : str
The name of the outcome variable in the dataframe.
"""
self.df = df
self.outcome_col = outcome_col
def plot_roc_curve(self, *pred_var_names):
"""
Plots the ROC curve(s) for the provided predictive variable(s).
Parameters:
*pred_var_names : str
Variable length argument list of predictive variable names.
"""
# create the figure for the plot
plt.figure(figsize=(8,6))
# check if more than one prediction variable is given
if len(pred_var_names) == 1:
# if only one variable, extract the number of variables and years
# from the name
num_vars = re.findall(r'\d+', pred_var_names[0])[0]
num_year = re.findall(r'\d+', pred_var_names[0])[-1]
title = 'AUC ROC: {}-Variable KFRE - {} Year Outcome'
else:
# if more than one variable, use a different title
title = 'AUC ROC: KFRE - Multiple Year Outcomes'
for pred_var_name in pred_var_names:
# compute ROC curve metrics
y_prob = self.df[pred_var_name]
fpr, tpr, _ = roc_curve(self.df[self.outcome_col], y_prob)
roc_auc = roc_auc_score(self.df[self.outcome_col], y_prob)
# plot the ROC curve
plt.plot(fpr, tpr, label=f'ROC curve for {pred_var_name} '
f'(AUC={roc_auc:.2f})')
# add labels and title to the plot
plt.plot([0, 1], [0, 1], 'r--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title(title.format(num_vars,
num_year) if len(pred_var_names) == 1 else title)
plt.legend(loc='lower right')
plt.show()
def report_metrics(self, pred_var_names):
"""
Calculates and reports various performance metrics for the provided
predictive variable(s).
Parameters:
pred_var_names : list
A list of predictive variable names.
Returns:
metrics_df : pandas.DataFrame
A dataframe containing the calculated performance metrics.
"""
metrics = {} # Initialize an empty dictionary to store metrics
metrics_order = ['Precision/PPV', 'PR AUC', 'Average Precision',
'Sensitivity', 'Specificity', 'AUC ROC',
'Brier Score'] # Metrics order
for prediction in pred_var_names:
# define true outcome and prediction
y_true = self.df[self.outcome_col]
y_pred = self.df[prediction]
# calculate various performance metrics
precision = precision_score(y_true, np.round(y_pred))
recall = recall_score(y_true, np.round(y_pred))
roc_auc = roc_auc_score(y_true, y_pred)
p_curve, r_curve, _ = precision_recall_curve(y_true, y_pred)
pr_auc = auc(r_curve, p_curve)
brier_score = brier_score_loss(y_true, y_pred)
try:
brier_score = brier_score_loss(y_true, y_pred)
except Exception as e:
print(f"Error calculating Brier Score: {e}")
brier_score = np.nan
avg_precision = average_precision_score(y_true, y_pred)
tn, fp, _, _ = confusion_matrix(y_true, np.round(y_pred)).ravel()
specificity = tn / (tn+fp)
# store the metrics in the dictionary
metrics[prediction] = {
'Precision/PPV': precision,
'PR AUC': pr_auc,
'Average Precision': avg_precision,
'Sensitivity': recall,
'Specificity': specificity,
'AUC ROC': roc_auc,
'Brier Score': brier_score,
}
# convert the metrics dictionary to a dataframe
metrics_df = pd.DataFrame(metrics).round(3)
# calculate the mean of the metrics and add it as a new column
metrics_df['Mean'] = metrics_df.mean(axis=1).round(3)
# enforce the order of the metrics
metrics_df = metrics_df.loc[metrics_order]
return metrics_df # Return the metrics DataFrame7.4.7 Plotting the ROC Curve
The plot_roc_curve function is important within the context of this research as it facilitates the visualization and evaluation of the performance of a prediction variable through the ROC (Receiver Operating Characteristic) curve.
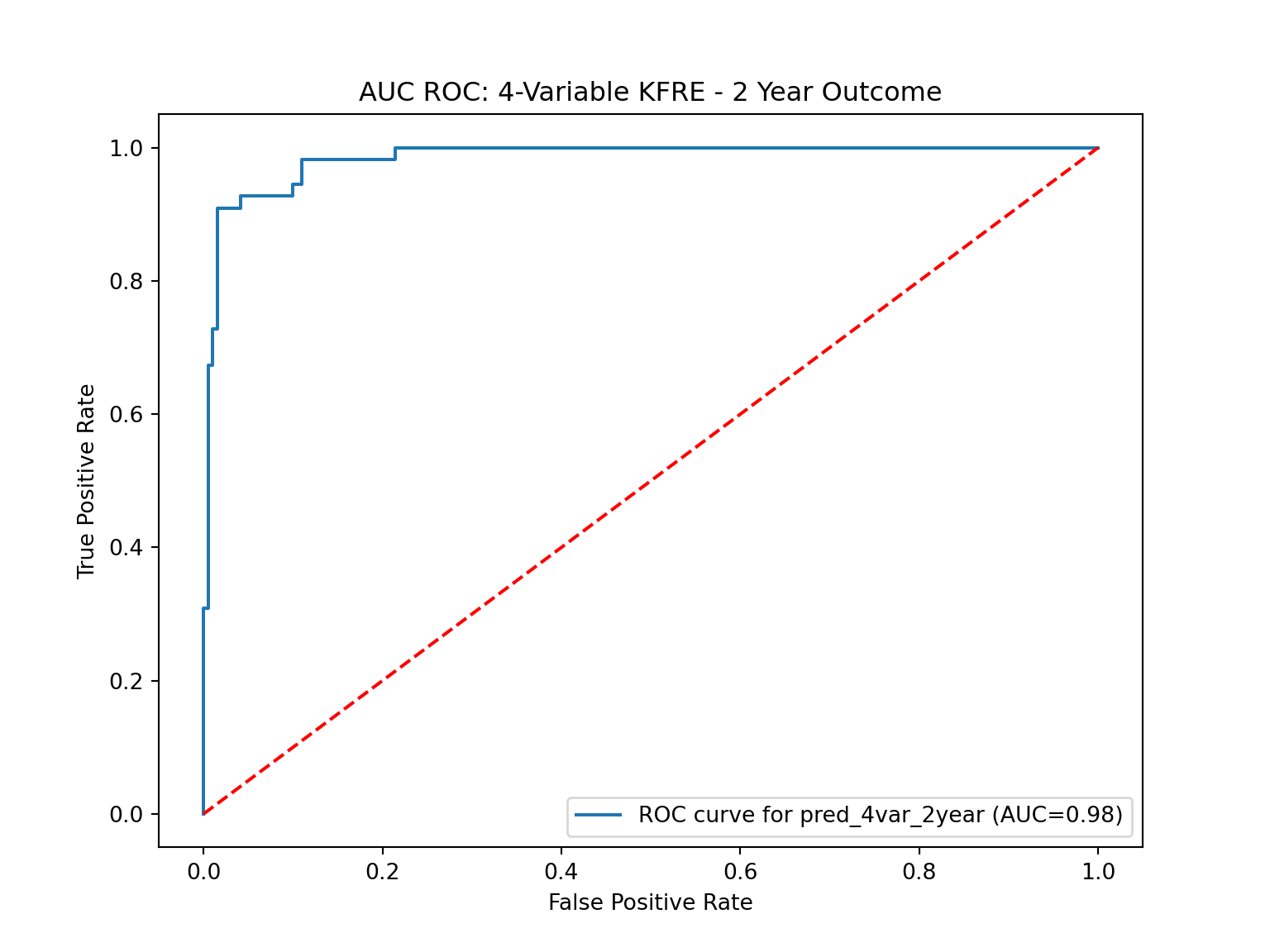
# Drop the mean column since we are only looking at one column
performance.report_metrics(['pred_4var_2year']).drop(columns='Mean')
# Remember, pred_var_names is a list of prediction columns. The plot_roc_curve()
# function is designed to take in the prediction columns as strings. So, rather
# than rehashing the same strings inside the list, we will unpack the list w/ *
performance.plot_roc_curve(*pred_var_names) # Plot all predictions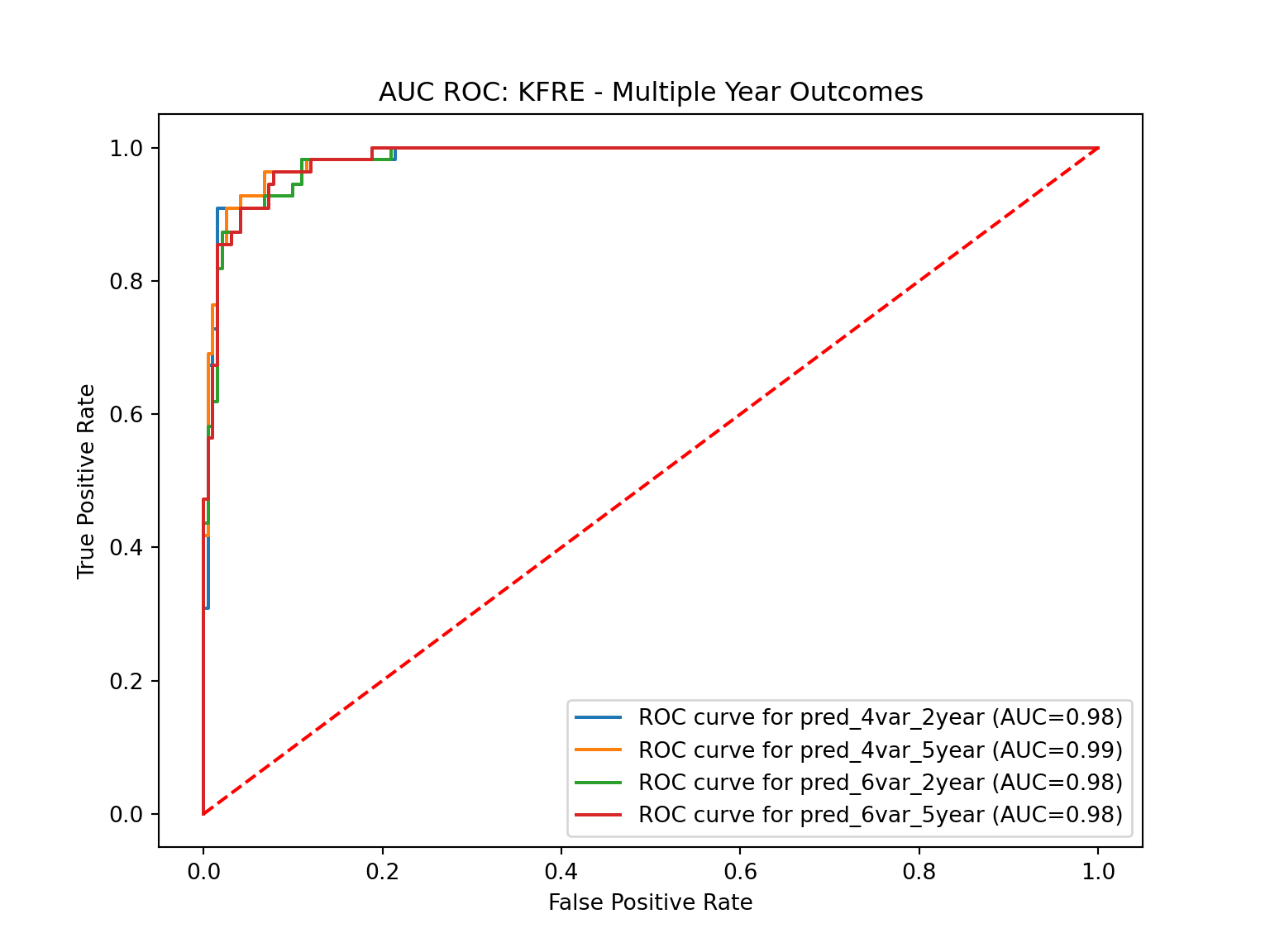
7.4.8 Model Results
Now, let’s review the performance of four distinct prediction models, each one displaying a robust ability to predict kidney failure events. We have a pair of 4-variable models projecting kidney failure events at 2-year and 5-year intervals, and a pair of 6-variable models with the same time frames.
Beginning with the measure of Precision or Positive Predictive Value (PPV), we find that all the models offer admirable predictive accuracy, with the 4-variable 2-year and 6-variable 2-year models leading with an impressive precision rate of approximately 96%. This measure indicates that the percentage of true positive predictions among all the positive predictions made by these models is exceedingly high, showing their reliability.
Turning to PR AUC (Precision-Recall Area Under the Curve) and Average Precision, we observe the models’ stability across different recall levels. These metrics serve as single-statistic summaries of the precision-recall curve, offering insight into how the models maintain their high precision even at varying recall levels. Our four models have nearly identical PR AUC and Average Precision scores, reflecting their consistent performance.
We next consider Sensitivity, also known as the true positive rate, which gives us the proportion of true positive predictions among all actual positives. While the 2-year models are somewhat less sensitive, the 5-year models achieve almost perfect sensitivity scores of around 96%. This might suggest that these models are particularly adept at longer-range predictions.
Looking at Specificity, our models prove capable of accurately identifying negative cases. The 2-year models excel in this area with scores approaching 99.5%, demonstrating their capacity to distinguish non-events accurately.
An overview of performance in binary classification tasks is best captured by the AUC ROC (Area Under the Receiver Operating Characteristics Curve) metric. All four of our models deliver near-perfect scores of around 98.4% here, reflecting their outstanding overall performance.
Lastly, we consider the Brier Score, which measures the mean squared difference between the predicted probability of an event and the actual outcome. The lower this score, the more accurately the model predicts. Our 5-year models outshine their 2-year counterparts in this regard, displaying lower Brier scores, indicating superior predictive accuracy.
In summary, our analysis reveals that these four models offer robust and reliable predictions, each demonstrating particular strengths. The 4-variable 2-year model excels in precision and specificity, while the 5-year models impress with their sensitivity and Brier scores. Hence, the ultimate selection of a model may well depend on the specific requirements of a clinical or research context, and which metrics are most critical to those scenarios.